Forecasting time series is a very common task in the daily life of a data scientist, which is surprisingly little covered in beginner machine learning courses.
It can be predicting future demand for a product, city traffic or even the weather.
With accurate time series forecasts, companies can adjust their production strategies, inventory management, resource allocation and other key decisions, leading to significant cost reduction and increased efficiency.
Furthermore, forecasts also allow companies to be more proactive rather than reactive, anticipating market trends and adjusting their strategies accordingly.
In this article you will learn how to forecast multiple time series easily with scikit-learn and the mlforecast library!
Installing MLForecast and Scikit-Learn
Instead of wasting time and making mistakes in manual data preparation, let’s use the mlforecast library.
It has tools that transform our raw time series data into the correct format for training and prediction with scikit-learn.
It computes the main features we want when modeling time series, such as aggregations over sliding windows, lags, differences, etc.
Finally, it implements a recursive prediction loop to forecast multiple steps into the future.
I will explain more about all this in the course of the article.
You can install the library with pip:
pip install mlforecast
pip install matplotlib
It will install scikit-learn, numpy and pandas too.
We will also need matplotlib to visualize the results.
The library is available in the Anaconda repository, but I recommend installing the pip version as it has the latest version.
How To Prepare Time Series Data for Scikit-Learn
We will use real sales data made available by Favorita, a large Ecuadorian grocery chain.
We have sales data from 2013 to 2017 for multiple stores and product categories.
import pandas as pd
import numpy as np
from matplotlib import pyplot as plt
path = 'train.csv'
data = pd.read_csv(path, index_col='id', parse_dates=['date'])
To run this example faster, we will only use the data from one store and two product categories.
So we have 2 time series to forecast, but this code can be used with as many time series as you want.
data2 = data.loc[(data['store_nbr'] == 1) & (data['family'].isin(['MEATS', 'PERSONAL CARE'])), ['date', 'family', 'sales', 'onpromotion']]
This data doesn’t contain a record for December 25, so I just copied the sales from December 18 to December 25 to keep the weekly pattern.
dec25 = list()
for year in range(2013,2017):
for family in ['MEATS', 'PERSONAL CARE']:
dec18 = data2.loc[(data2['date'] == f'{year}-12-18') & (data2['family'] == family)]
dec25 += [{'date': pd.Timestamp(f'{year}-12-25'), 'family': family, 'sales': dec18['sales'].values[0], 'onpromotion': dec18['onpromotion'].values[0]}]
data2 = pd.concat([data2, pd.DataFrame(dec25)], ignore_index=True).sort_values('date')
data2 = data2.rename(columns={'date': 'ds', 'sales': 'y', 'family': 'unique_id'})
The columns are:
date: date of the recordfamily: product categorysales: number of salesonpromotion: number of products of that category that were on promotion on that day
To keep Nixtla’s (the creator of mlforecast) libraries standard format, let’s rename the columns to ds (date), y (target) and unique_id (family).
unique_id should identify each time series you have.
If we had more than one store, we would have to add the store number along with the categories to unique_id.
An example would be unique_id = store_nbr + '_' + family.
This is the final version of our dataframe data2:
| ds | unique_id | y | onpromotion |
|---|---|---|---|
| 2013-01-01 00:00:00 | MEATS | 0 | 0 |
| 2013-01-01 00:00:00 | PERSONAL CARE | 0 | 0 |
| 2013-01-02 00:00:00 | MEATS | 369.101 | 0 |
| 2013-01-02 00:00:00 | PERSONAL CARE | 194 | 0 |
| 2013-01-03 00:00:00 | MEATS | 272.319 | 0 |
A row for each record containing the date, the time series ID (family in our example), the target value and columns for external variables (onpromotion).
Notice the time series records are stacked on top of each other.
Let’s split the data into train and validation sets.
Time Series Validation
You should never use random or k-fold validation for time series.
That would cause data leakage, as you would be using future data to train your model.
In practice, you can’t take random samples from the future to train your model, so you can’t use them here.
To avoid this issue, we will use a simple time series split between past and future.
A career tip: knowing how to do time series validation correctly is a skill that will set you apart from many data scientists (even experienced ones!).
Our training set will be all the data between 2013 and 2016 and our validation set will be the first 3 months of 2017.
train = data2.loc[data2['ds'] < '2017-01-01']
valid = data2.loc[(data2['ds'] >= '2017-01-01') & (data2['ds'] < '2017-04-01')]
Feature Engineering for Time Series Forecasting
Now that we have our data formatted according to what mlforecast expects, let’s define the features we are going to use.
This is a crucial step for the success of your model.
I usually think of 4 main types of features for time series. You can calculate them using the target or external variables:
Lags
Lags are simply past values of the time series that you shift forward to use as features in the model.
For example, if you want to predict the demand of a product next week, you can use the demand of the same weekday in the previous week as a feature.
In practice, the demand of a product on a given day of the week is similar in different weeks, so this feature can be useful for the model.
You can also use longer lags, like the demand of the same day in the previous month or year.
It’s important to test different lags to find the ones that work best for your specific problem.
Don’t be afraid of adding lots of lag features!
No one can tell you which lags are the best for your problem without testing.
Rolling Window Aggregations
Rolling window aggregations are statistical functions applied to records in a sliding window.
They can be calculated over expanding windows too, but sliding windows are usually more robust in practice.
An example is calculating the average daily demand of the last 7 days, or the standard deviation of the returns of a financial asset over the last 4 weeks.
These features can help the model identify trends in the time series.
Like lags, it’s important to test different aggregation functions and window sizes to find the ones that work best for your specific problem.
Date Components
Date components are values you extract from a specific date or timestamp.
For example, you can include the hour of the day, the day of the week, the month, the season of the year, etc.
These features can help the model identify seasonal and cyclical patterns in the time series.
As with other features, test different components and find the ones that work best.
Differences
Differences are simply the subtraction of two values in a time series.
An example is the difference between the demand of today and the demand of yesterday.
Even though we have lags, having differences as features can bring specific information the model needs to more easily identify patterns.
Feature engineering is a lot about making the patterns in the data more explicit for the model.
Feature Engineering Code
Now that we know the features we want to use, let’s compute them with the mlforecast library.
First, we need to create a list with the scikit-learn models we want to test.
from sklearn.ensemble import RandomForestRegressor, ExtraTreesRegressor
models = [RandomForestRegressor(random_state=0, n_estimators=100),
ExtraTreesRegressor(random_state=0, n_estimators=100)]
I will test only 2 models, the Random Forest and the Extra Trees, but you can test as many models as you want. Just add them to the list.
At the time of writing, mlforecast and window_ops don’t support calculating difference features, so I created the diff function using numba.
from numba import njit
@njit
def diff(x, lag):
x2 = np.full_like(x, np.nan)
for i in range(lag, len(x)):
x2[i] = x[i] - x[i-lag]
return x2
numba is a library that optimizes your Python code to run faster and it’s recommended by the mlforecast developers when creating custom functions to compute features.
We need to add the @njit decorator to the function to tell numba to compile it.
The function gets two arguments, x and lag.
x is an array and lag is the number of periods we want to use to calculate the difference.
The first line inside the function creates a new array x2 with the same format as the array x, but all the values are initialized as NaN.
Inside the loop, we will set the values of x2 to the difference between the values in x and the values in x shifted by lag periods.
If it’s a lag of 3, for example, the value in position 3 of x2 is the difference between the value in position 3 and the value in position 0 of x.
The function returns the array x2 with the differences for each period.
Now we will create the object that manages the creation of the features and the training of the models.
from window_ops import rolling_mean
from mlforecast import MLForecast
model = MLForecast(models=models,
freq='D',
lags=[1,7,14],
lag_transforms={
1: [(rolling_mean, 3), (rolling_mean, 7), (rolling_mean, 28), (diff, 1), (diff, 7)],
},
date_features=['dayofweek'],
num_threads=6)
MLForecast is the object that will make our work easier.
It manages feature engineering and model training.
The first argument, models, is the list with the models we want to train.
The second is freq, which indicates the frequency of the time series. Daily in our example.
The third argument, lags=[1,7,14], indicates the lag values we want to use as features. We will use lags of 1, 7 and 14 days.
The fourth argument, lag_transforms={...}, is a dictionary with the functions we want to apply to the lags.
The keys in the dictionary are the lag series to which the functions will be applied.
We will calculate a rolling mean of lag 1 with windows of 3, 7 and 28 days, and the difference between the current value and the value 1 and 7 days before.
Just remember that “current value” is the series value at the lag, not the value of the current time step, as the latter is the value we want to predict.
In our example, the 7-day rolling mean is computed using lag 1 as the most recent value, and so on.
The functions will get an array with the original time series shifted by the lag value in the same order as the original dataframe.
Usually it’s from the oldest record to the newest.
Then we set date_features=['dayofweek'] to specify which date components we want to extract. I used only the day of the week.
Finally, we set num_threads=6 to specify how many threads should be used to process the data in parallel.
I used 6 because I have a 6-core CPU, but you can use as many threads as you want.
Remember that we still have the onpromotion feature, which is an external variable related to the target.
Any columns besides the target, the ID and the date will be considered as external variables.
By default it considers them as static features, which means they don’t change over time (like a product brand or the store city).
During prediction it generates a dataframe with the same values for all the time steps.
We can explicitly tell which columns are static features with the static_features argument in the fit method.
Even if you don’t have any static features but have dynamic features, it’s important to pass an empty list to this argument, because MLForecast will think your dynamic features are static and ignore its new values if you don’t do that.
model.fit(train, id_col='unique_id', time_col='ds', target_col='y', static_features=[])
p = model.predict(horizon=90, dynamic_dfs=[valid[['unique_id', 'ds', 'onpromotion']]])
p = p.merge(valid[['unique_id', 'ds', 'y']], on=['unique_id', 'ds'], how='left')
In the fit method, we pass the training dataframe, the names of the columns with the ID of the time series, date, target, and the list with the names of static features.
In the predict method, we pass the number of time steps we want to predict (horizon) and a list with dataframes with the values of the dynamic features for the periods we want to predict.
The number of time steps is counted from the last date in the training dataframe.
In our case, we know which products will be on promotion in the next 90 days (we can plan it), so we can pass a dataframe with the onpromotion column for the next 90 days.
We could even use this model to simulate the impact of a promotion on sales by setting the onpromotion column to 1 for arbitrary periods in the future.
But if we had external variables that we don’t know in advance (like temperature), we would need to use estimates.
A very common mistake is to use historical values of the external variables during validation without considering that they won’t be available at the time of prediction in production.
This shows you an overly optimistic estimate of the model performance, which won’t be real in practice.
That’s why it’s important to create these features here using the same process that will be used in production.
It’s important that the dataframes with the external variables have columns that can be used to merge it with the main dataframe.
At a minimum the date of the record and potentially any others that ID the time series.
Thinking about temperature again, we could have the city code as a static feature, and an external variables dataframe with the city code, date and temperature estimates for the prediction period.
The last line merges the predictions with the validation dataframe to make it easier to calculate the error and visualize the results.
The predictions for each model are stored in a column with the name of the model object.
| unique_id | ds | RandomForestRegressor | ExtraTreesRegressor | y |
|---|---|---|---|---|
| MEATS | 2017-01-01 00:00:00 | 149.719 | 115.594 | 0 |
| PERSONAL CARE | 2017-01-01 00:00:00 | 83.1048 | 64.9456 | 0 |
| PERSONAL CARE | 2017-01-02 00:00:00 | 138.117 | 154.29 | 81 |
| MEATS | 2017-01-02 00:00:00 | 245.477 | 267.907 | 116.724 |
| MEATS | 2017-01-03 00:00:00 | 274.266 | 267.524 | 344.583 |
Checking For Data Leakage in Features
It’s very important to check if the features were computed correctly, without data leakage (like using the target instead of a lag to compute a difference).
We can use the preprocess method. It returns a dataframe with the features computed for the training data.
model.preprocess(train, id_col='unique_id', time_col='ds', target_col='y', static_features=[])
| ds | unique_id | y | onpromotion | lag1 | lag7 | lag14 | rolling_mean_lag1_window_size3 | rolling_mean_lag1_window_size7 | rolling_mean_lag1_window_size28 | diff_lag1_lag1 | diff_lag1_lag7 | dayofweek |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2013-01-29 00:00:00 | MEATS | 260.633 | 0 | 325.072 | 274.261 | 287.346 | 289.11 | 311.035 | 296.329 | 57.256 | 50.186 | 1 |
| 2013-01-29 00:00:00 | PERSONAL CARE | 91 | 0 | 107 | 90 | 95 | 88.6667 | 88.7143 | 98.5357 | 65 | 18 | 1 |
| 2013-01-30 00:00:00 | MEATS | 304.018 | 0 | 260.633 | 312.199 | 369.492 | 284.507 | 309.088 | 305.637 | -64.439 | -13.628 | 2 |
| 2013-01-30 00:00:00 | PERSONAL CARE | 98 | 0 | 91 | 103 | 118 | 80 | 88.8571 | 101.786 | -16 | 1 | 2 |
| 2013-01-31 00:00:00 | MEATS | 264.937 | 0 | 304.018 | 215.607 | 280.879 | 296.574 | 307.92 | 303.313 | 43.385 | -8.181 | 3 |
Pick a few samples and manually compute the values of the features in the original series to check if the values computed by MLForecast are correct.
Recursive vs Direct Forecasting
There are at least 3 different ways to generate forecasts when you use machine learning for time series.
The default way in MLForecast is to use the recursive or auto-regressive method.
To understand this method, imagine a time series with only 10 observations and a model trained to predict only 1 step ahead.
To get predictions for multiple periods, we will add the next step prediction into the original series as if it was a new sample and use the model to predict the next period.
We repeat these steps for the next periods until we have predictions for the full horizon we want to predict
As an alternative, we can use the direct method, which trains a separate, individual model, for each step of the forecast horizon.
So if we want to predict 10 periods, we train 10 models, each one to predict a specific step.
The recursive method is faster to train, especially if you have a large forecast horizon.
There is no way to know which method is better without testing, so if you need the best performance, even if the computational cost is high, test both.
To use the direct method in MLForecast, just pass the max_horizon argument in the fit method with the number of periods you want to predict.
model.fit(train, id_col='unique_id', time_col='ds', target_col='y',
static_features=[], max_horizon=90)
Retrieving Feature Importances
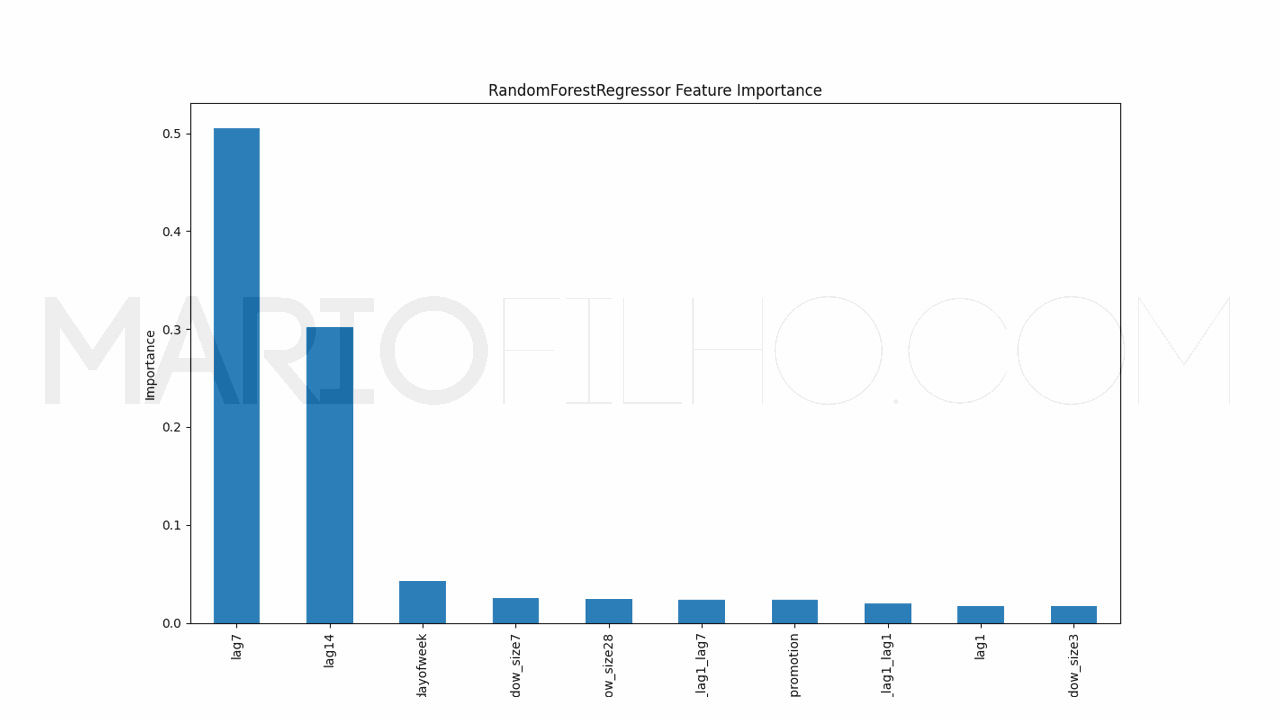
To understand how the model is making its decisions, we can use the internal calculation of feature importances.
It’s very simple to get them using the feature_importances_ attribute of the model.
pd.Series(model.models_['RandomForestRegressor'].feature_importances_, index=model.ts.features_order_).sort_values(ascending=False).plot.bar(
figsize=(1280/96,720/96), title='RandomForestRegressor Feature Importance', xlabel='Features', ylabel='Importance')
Here we will see a bar chart with the features on the X axis and their importance on the Y axis. A higher bar means the model considers this feature more important when generating the forecast.
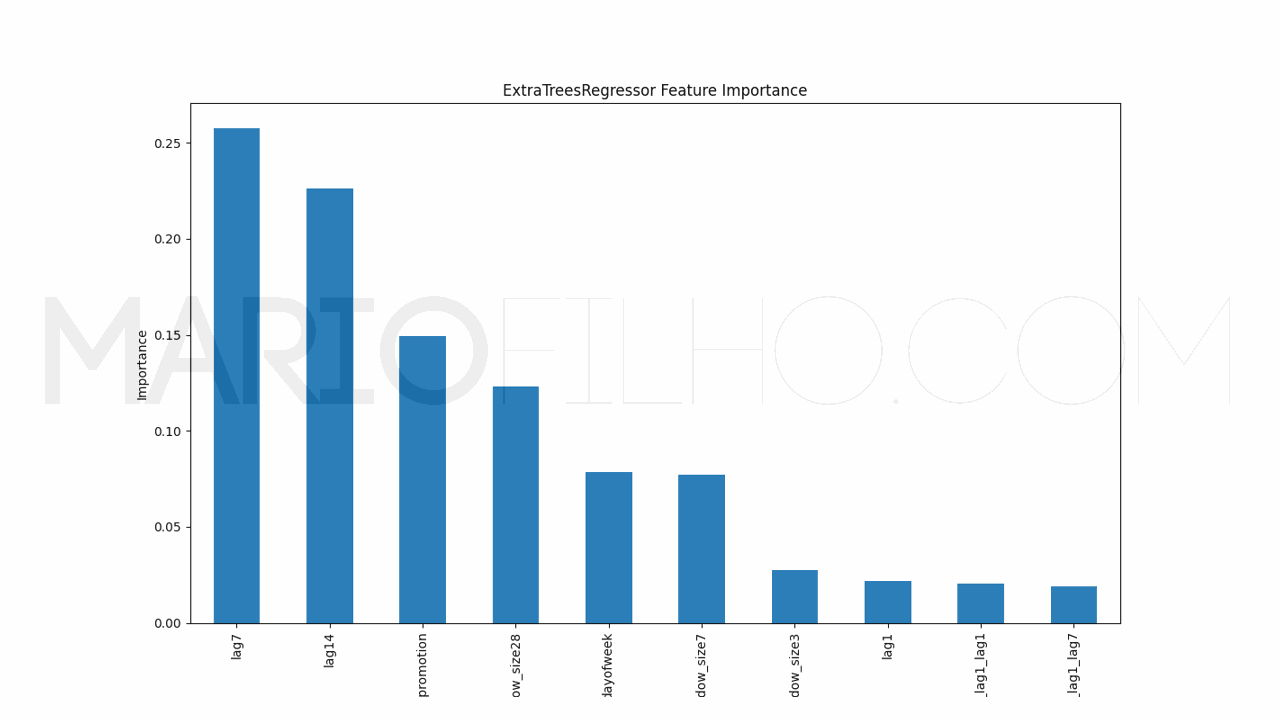
How To Measure Forecast Accuracy
We can compute the error using any metric we want, as we do when normally using scikit-learn.
I created a custom function to calculate WMAPE, which is an adaptation of the mean absolute percentage error that solves the problem of dividing by zero.
The weight of each sample is given by the magnitude of the real value.
Here’s the function for the simplified version of the metric:
def wmape(y_true, y_pred):
return np.abs(y_true - y_pred).sum() / np.abs(y_true).sum()
print(f"WMAPE RandomForestRegressor: {wmape(p['y'], p['RandomForestRegressor'])}\nWMAPE ExtraTreesRegressor: {wmape(p['y'], p['ExtraTreesRegressor'])}")
In our dataset, RandomForestRegressor had an error of 18.78% and ExtraTreesRegressor got 17.98%.
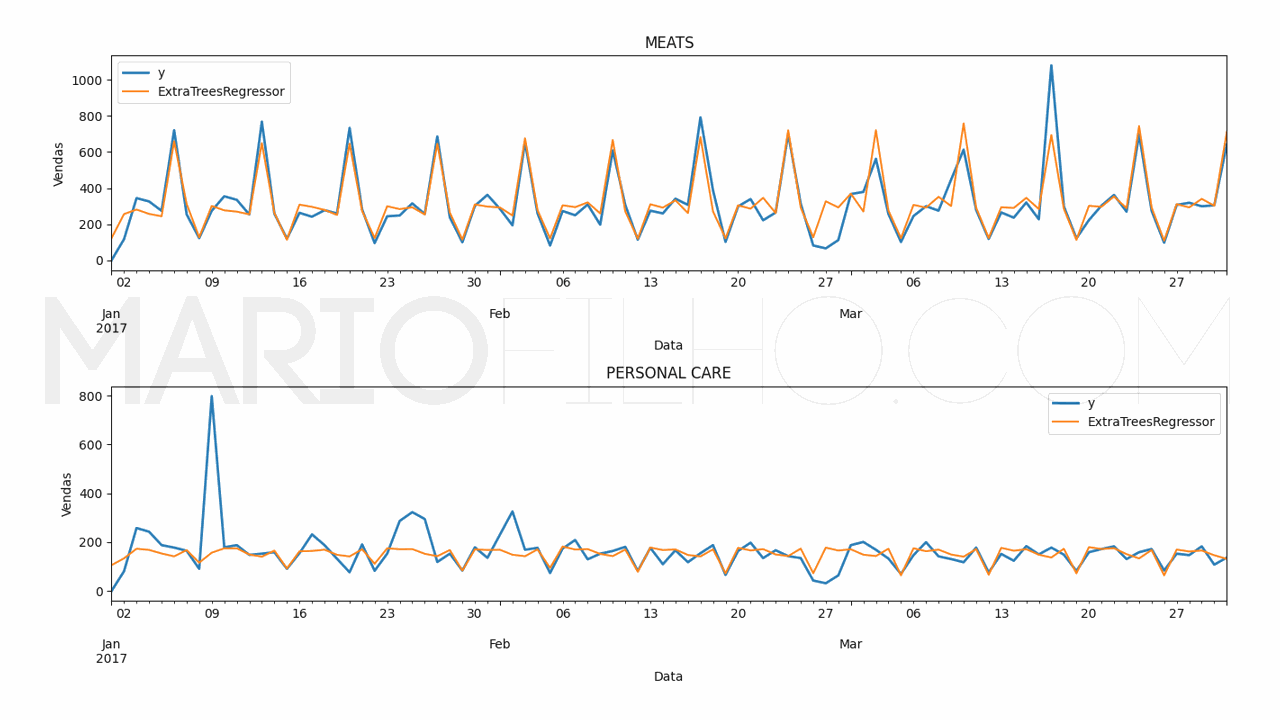
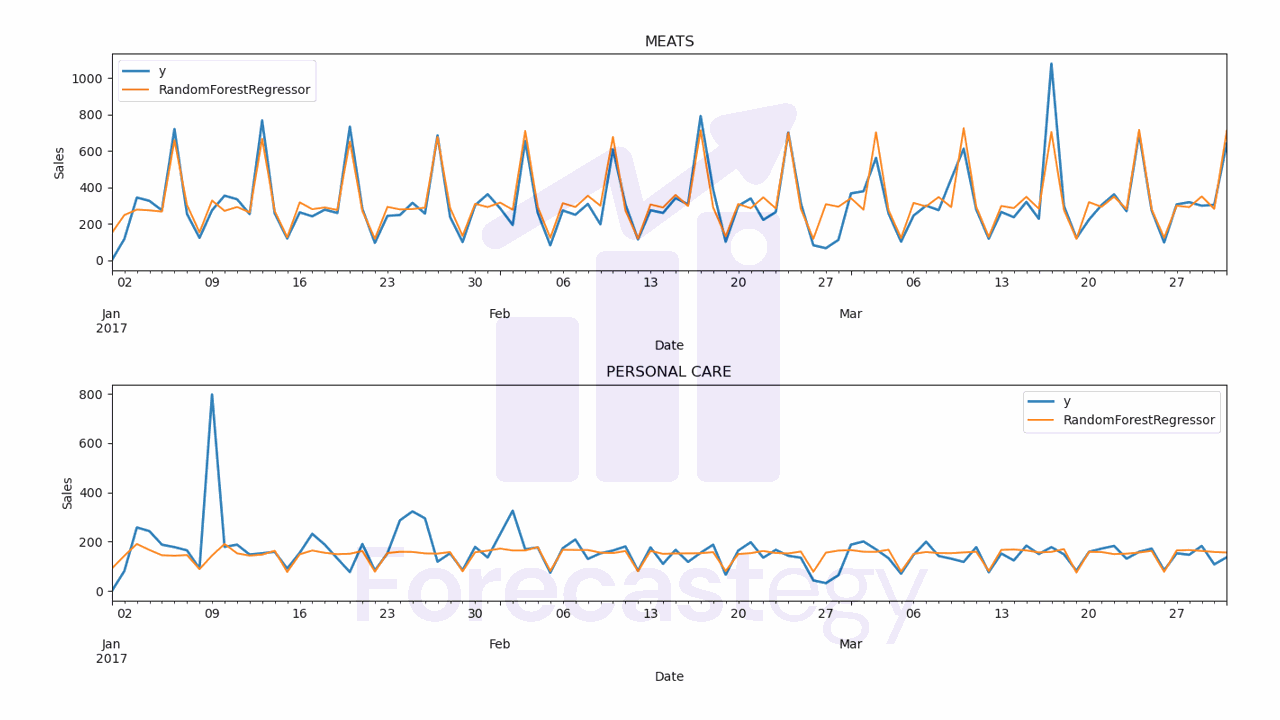
The code to plot the forecast:
for model in ['RandomForestRegressor', 'ExtraTreesRegressor']:
fig,ax = plt.subplots(2,1, figsize=(1280/96, 720/96))
for ax_, family in enumerate(['MEATS', 'PERSONAL CARE']):
p.loc[p['unique_id'] == family].plot(x='ds', y='y', ax=ax[ax_], label='y', title=family, linewidth=2)
p.loc[p['unique_id'] == family].plot(x='ds', y=model, ax=ax[ax_], label=model)
ax[ax_].set_xlabel('Date')
ax[ax_].set_ylabel('Sales')
fig.tight_layout()
Frequently Asked Questions
How To Use MLForecast With Multiple SKUs?
The only change is that your unique_id column will be the SKU. You can use the rest of the code as is.
How To Train An XGBoost Model?
Check the article about multiple time series forecasting with XGBoost.
Can You Train an LSTM Using Scikit-Learn?
No. Although scikit-learn has a very limited implementation of multi-layer feedforward neural networks, there is no implementation of recurrent neural networks.